Matriz inversa.
Matriz inversa.
Entender los conceptos elementales del álgebra lineal y los aplicará en problemas del ámbito económico y de gestión de negocios.Matriz de dos filas (Matriz Adjunta)
Dada una matriz de 2x2 con determinante no nulo:Está definida siempre y cuando
 . Así por ejemplo la inversa de la matriz
. Así por ejemplo la inversa de la matrizDada una matriz de 3x3 con determinante no nulo:ya que
Propiedades de la matriz inversa
- La inversa de una matriz, si existe, es única.
- La inversa del producto de dos matrices es el producto de las inversas cambiando el orden:
- Si la matriz es invertible, también lo es su transpuesta, y el inverso de su transpuesta es la transpuesta de su inversa, es decir:
- Y, evidentemente:
- Una matriz es invertible si y sólo si el determinante de A es distinto de cero. Además la inversa satisface la igualdad:
 es el determinante de A y
es el determinante de A y  es la matriz de adjuntos de A.
es la matriz de adjuntos de A.Demostración de la unicidad de la inversa
Supongamos que B y C son inversas de ADemostración del criterio de inversibilidad de las matrices cuadradas
Se probará la doble implicación.
Suficiencia 
Suponiendo que existe  tal que
tal que  . Entonces al aplicar la función determinante se obtiene
. Entonces al aplicar la función determinante se obtiene
 es distinto de cero.
es distinto de cero.
Necesidad 
Suponiendo que el determinante de  es distinto de cero, sea
es distinto de cero, sea 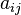 es el elemento ij de la matriz
es el elemento ij de la matriz  y sea
y sea  la matriz
la matriz  sin la fila
sin la fila  y la columna
y la columna  (comúnmente conocida como
(comúnmente conocida como  -ésimo menor de A). Entonces
-ésimo menor de A). Entonces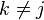 , entonces
, entonces con la columna
con la columna  igual a la columna
igual a la columna  y los demás términos iguales a los de
y los demás términos iguales a los de  . Entonces
. Entonces cuando
cuando 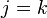 y
y  cuando
cuando 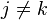 . Entonces
. Entonces tiene inversa izquierda
tiene inversa izquierda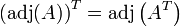 , entonces
, entonces  también tiene inversa izquierda que es
también tiene inversa izquierda que esMétodos de inversión de matrices
Solución analítica
Inversión de matrices 2×2
Calcular la matriz inversa en matrices de 2x2 puede ser muy sencillo. Se puede hacer de la siguiente manera:1Ejemplo numérico:
Inversión de matrices de órdenes superiores
Para matrices de órdenes superiores puede utilizarse la siguiente fórmula: es el determinante de A y
es el determinante de A y 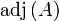 es la matriz de adjuntos de A.
es la matriz de adjuntos de A.Cuando la matriz tiene más de tres filas, está fórmula es muy ineficiente y conduce a largos cálculos. Hay métodos alternativos para calcular la matriz inversa que son bastante más eficientes.
Métodos numéricos
El método de eliminación de Gauss-Jordan puede utilizarse para determinar si una determinada matriz es invertible y para encontrar su inversa. Una alternativa es la descomposición LU, que descompone una matriz dada como producto de dos matrices triangulares, una inferior y otra superior, mucho más fáciles de invertir. Utilizando el método de Gauss-Jordan se coloca a la izquierda la matriz dada y a la derecha la matriz identidad. Luego por medio del uso de pivotes se intenta formar en la izquierda la matriz identidad y la matriz que quede a la derecha será la matriz inversa a la dada.Grupo lineal
El conjunto de todas las matrices que admiten inversa se denota es una representación lineal del grupo lineal de orden n, denotado como
que admiten inversa se denota es una representación lineal del grupo lineal de orden n, denotado como 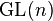 . Este grupo tiene importantes aplicaciones en álgebra y física. Además
. Este grupo tiene importantes aplicaciones en álgebra y física. Además 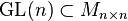 es un conjunto abierto (con la topología inducida de
es un conjunto abierto (con la topología inducida de  ).
).| ARYA, J. C. (2009). Matemáticas aplicadas a la administración. México: Pearson Educacíon. |
| (2015). Matriz inversa.En: wikiped… Consultado elSábado, 14 de noviembre de 2015 Se encuentra en: https://es.wikipedia.org/wiki/Matriz_invertible |
.png)

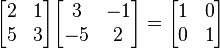


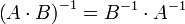




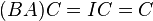


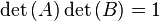

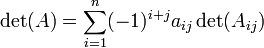
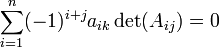


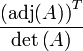



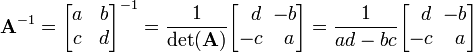

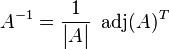


0 comentarios: