Integral de una suma (diferencia) de funciones.
Integral de una suma (diferencia) de funciones. |
Entender el concepto de integral y su relación con la derivada. Resolverá problemas de aplicación dando énfasis a aquellos relacionados con las áreas económico-administrativas tales como: Economía, Mercadotecnia, Administración, Turismo, Recursos Humanos, Sistemas de Información y Negocios Internacionales.
La integración es un concepto fundamental del cálculo y del análisis matemático. Básicamente, una integral es una generalización de la suma de infinitos sumandos, infinitamente pequeños.
El cálculo integral, encuadrado en el cálculo infinitesimal, es una rama de las matemáticas en el proceso de integración o antiderivación, es muy común en la ingeniería y en la ciencia también; se utiliza principalmente para el cálculo de áreas y volúmenes de regiones y sólidos de revolución.
Fue usado por primera vez por científicos como Arquímedes, René Descartes, Isaac Newton, Gottfried Leibniz e Isaac Barrow. Los trabajos de este último y los aportes de Newton generaron el teorema fundamental del cálculo integral, que propone que la derivación y la integración son procesos inversos.
Índice
- 1 Principales objetivos del cálculo integral
- 2 Teoría
- 3 Historia
- 4 Terminología y notación
- 5 Conceptos y aplicaciones
- 6 Definiciones formales
- 7 Propiedades de la integración
- 8 Teorema fundamental del cálculo
- 9 Extensiones
- 10 Métodos y aplicaciones
- 11 Algunas aplicaciones
- 12 Véase también
- 13 Referencias y notas
- 14 Bibliografía
- 15 Enlaces externos
Principales objetivos del cálculo integral
Sus principales objetivos a estudiar son:- Área de una región plana
- Cambio de variable
- Integrales indefinidas
- Integrales definidas
- Integrales impropias
- Integral de línea
- Integrales múltiples (dobles o triples)
- Integrales trigonométricas, logarítmicas y exponenciales
- Métodos de integración
- Teorema fundamental del cálculo
- Volumen de un sólido de revolución
Teoría
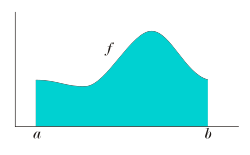
 se interpreta como el área bajo la curva de f, entre a y b.
se interpreta como el área bajo la curva de f, entre a y b. de una variable real
de una variable real  y un intervalo
y un intervalo ![[a,b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) de la recta real, la integral es igual al área de la región del plano
de la recta real, la integral es igual al área de la región del plano  limitada entre la gráfica de
limitada entre la gráfica de  , el eje
, el eje  , y las líneas verticales
, y las líneas verticales  y
y 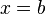 , donde son negativas las áreas por debajo del eje
, donde son negativas las áreas por debajo del eje  .
.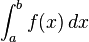
La palabra "integral" también puede hacer referencia a la noción de primitiva: una función F, cuya derivada es la función dada
 . En este caso se denomina integral indefinida, mientras que las integrales tratadas en este artículo son las integrales definidas. Algunos autores mantienen una distinción entre integrales primitivas e indefinidas.
. En este caso se denomina integral indefinida, mientras que las integrales tratadas en este artículo son las integrales definidas. Algunos autores mantienen una distinción entre integrales primitivas e indefinidas.Los principios de la integración fueron formulados por Newton y Leibniz a finales del siglo XVII. A través del teorema fundamental del cálculo, que desarrollaron los dos de forma independiente, la integración se conecta con la derivación, y la integral definida de una función se puede calcular fácilmente una vez se conoce una antiderivada. Las integrales y las derivadas pasaron a ser herramientas básicas del cálculo, con numerosas aplicaciones en ciencia e ingeniería.
Bernhard Riemann dio una definición rigurosa de la integral. Se basa en un límite que aproxima el área de una región curvilínea a base de partirla en pequeños trozos verticales. A comienzos del siglo XIX, empezaron a aparecer nociones más sofisticadas de la integral, donde se han generalizado los tipos de las funciones y los dominios sobre los cuales se hace la integración. La integral curvilínea se define para funciones vectoriales de una variable, y el intervalo de integración [a,b] se sustituye por el de la parametrización de la curva sobre la cual se está integrando, la cual, conecta dos puntos del plano o del espacio. En una integral de superficie, la curva se sustituye por un trozo de una superficie en el espacio tridimensional.
Las integrales de las formas diferenciales desempeñan un papel fundamental en la geometría diferencial moderna. Estas generalizaciones de la integral surgieron primero a partir de las necesidades de la física, y tienen un papel importante en la formulación de muchas leyes físicas cómo, por ejemplo, las del electromagnetismo. Los conceptos modernos de integración se basan en la teoría matemática abstracta conocida como integral de Lebesgue, que fue desarrollada por Henri Lebesgue.
Historia
Integración antes del cálculo
La integración se puede trazar en el pasado hasta el antiguo Egipto, circa 1800 a. C., con el papiro de Moscú, donde se demuestra que ya se conocía una fórmula para calcular el volumen de un tronco piramidal. La primera técnica sistemática documentada capaz de determinar integrales es el método de exhausción de Eudoxo (circa 370 a. C.), que trataba de encontrar áreas y volúmenes a base de partirlos en un número infinito de formas para las cuales se conocieran el área o el volumen. Este método fue desarrollado y usado más adelante por Arquímedes, que lo empleó para calcular áreas de parábolas y una aproximación al área del círculo. Métodos similares fueron desarrollados de forma independiente en China alrededor del siglo III por Liu Hui, que los usó para encontrar el área del círculo. Más tarde, Zu Chongzhi usó este método para encontrar el volumen de una esfera. En el Siddhanta Shiromani, un libro de astronomía del siglo XII del matemático indio Bhaskara II, se encuentran algunas ideas de cálculo integral.Hasta el siglo XVI no empezaron a aparecer adelantos significativos sobre el método de exhausción. En esta época, por un lado, con el trabajo de Cavalieri con su método de los indivisibles y, por otro lado, con los trabajos de Fermat, se empezó a desarrollar los fundamentos del cálculo moderno. A comienzos del siglo XVII, se produjeron nuevos adelantos con las aportaciones de Barrow y Torricelli, que presentaron los primeros indicios de una conexión entre la integración y la derivación.
Newton y Leibniz
Los principales adelantos en integración vinieron en el siglo XVII con la formulación del teorema fundamental del cálculo, realizado de manera independiente por Newton y Leibniz. El teorema demuestra una conexión entre la integración y la derivación. Esta conexión, combinada con la facilidad, comparativamente hablando, del cálculo de derivadas, se puede usar para calcular integrales. En particular, el teorema fundamental del cálculo permite resolver una clase más amplia de problemas. También cabe destacar todo el marco estructural alrededor de las matemáticas que desarrollaron también Newton y Leibniz. El llamado cálculo infinitesimal permitió analizar, de forma precisa, funciones con dominios continuos. Posteriormente, este marco ha evolucionado hacia el cálculo moderno, cuya notación para las integrales procede directamente del trabajo de Leibniz.Formalización de las integrales
Aunque Newton y Leibniz proporcionaron un enfoque sistemático a la integración, su trabajo carecía de un cierto nivel de rigor. Es memorable el ataque del obispo Berkeley calificando los infinitesimales como los "fantasmas de las cantidades que se desvanecen".El cálculo adquirió una posición más firme con el desarrollo de los límites y, en la primera mitad del siglo XIX, recibió una fundamentación adecuada por parte de Cauchy. La integración fue rigurosamente formalizada por primera vez por Riemann, empleando límites. A pesar de que todas las funciones continuas fragmentadas y acotadas son integrables en un intervalo acotado, más tarde se consideraron funciones más generales para las cuales la definición de Riemann no era aplicable y por tanto no eran integrables en el sentido de Riemann. Posteriormente Lebesgue dio una definición diferente de la integral1 basada en la teoría de la medida que generalizaba la definición de Riemann, así toda función integrable en el sentido de Riemann también lo es en el sentido de Lebesgue, aunque existen algunas funciones integrables en el sentido de Lebesgue que no lo son en el sentido de Riemann. Más recientemente se han propuesto otras definiciones de integral aún más generales, que amplían las definiciones de Riemann y Lebesgue.
Notación
Isaac Newton usaba una pequeña barra vertical encima de una variable para indicar integración, o ponía la variable dentro de una caja. La barra vertical se confundía fácilmente con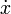 o
o 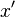 ,
que Newton usaba para indicar la derivación, y además la notación
"caja" era difícil de reproducir por los impresores; por ello, estas
notaciones no fueron ampliamente adoptadas.
,
que Newton usaba para indicar la derivación, y además la notación
"caja" era difícil de reproducir por los impresores; por ello, estas
notaciones no fueron ampliamente adoptadas.La notación moderna de las integrales indefinidas fue presentada por Gottfried Leibniz en 1675.2 3 Para indicar summa (ſumma; en latín, "suma" o "total"), adaptó el símbolo integral, "∫", a partir de una letra S alargada. La notación moderna de la integral definida, con los límites arriba y abajo del signo integral, la usó por primera vez Joseph Fourier en Mémoires de la Academia Francesa, alrededor de 1819–20, reimpresa en su libro de 1822.4 5 En la notación matemática en árabe moderno, que se escribe de derecha a izquierda, se usa un signo integral invertido
Terminología y notación
Si una función tiene una integral, se dice que es integrable. De la función de la cual se calcula la integral se dice que es el integrando. Se denomina dominio de integración a la región sobre la cual se integra la función. Si la integral no tiene un dominio de integración, se considera indefinida (la que tiene dominio se considera definida). En general, el integrando puede ser una función de más de una variable, y el dominio de integración puede ser un área, un volumen, una región de dimensión superior, o incluso un espacio abstracto que no tiene estructura geométrica en ningún sentido usual.El caso más sencillo, la integral de una función real f de una variable real x sobre el intervalo [a, b], se escribe
Conceptos y aplicaciones
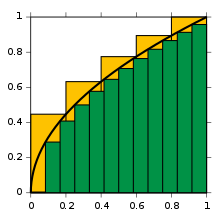
Aproximaciones a la integral de  entre 0 y 1, con ■ 5 muestras por la izquierda (arriba) y ■ 12 muestras por la derecha (abajo).
entre 0 y 1, con ■ 5 muestras por la izquierda (arriba) y ■ 12 muestras por la derecha (abajo).
 entre 0 y 1, con ■ 5 muestras por la izquierda (arriba) y ■ 12 muestras por la derecha (abajo).
entre 0 y 1, con ■ 5 muestras por la izquierda (arriba) y ■ 12 muestras por la derecha (abajo).Para el cálculo integral de áreas se sigue el siguiente razonamiento:
- Por ejemplo, consideremos la curva mostrada en la figura de arriba, gráfica de la función
 , acotada entre
, acotada entre 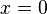 y
y 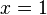 .
. - La respuesta a la pregunta ¿Cuál es el área bajo la curva de función
 , en el intervalo desde
, en el intervalo desde  hasta
hasta  ? es: que el área coincidirá con la integral de
? es: que el área coincidirá con la integral de  . La notación para esta integral será
. La notación para esta integral será
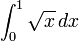 .
.
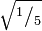 ,
, 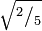 ,
, 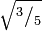 … y así hasta
… y así hasta 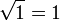 . Sumando las áreas de estos rectángulos, se obtiene una segunda aproximación de la integral que se está buscando,
. Sumando las áreas de estos rectángulos, se obtiene una segunda aproximación de la integral que se está buscando,Con respecto al cálculo real de integrales, el teorema fundamental del cálculo, debido a Newton y Leibniz, es el vínculo fundamental entre las operaciones de derivación e integración. Aplicándolo a la curva raíz cuadrada, se tiene que mirar la función relacionada
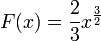 y simplemente tomar
y simplemente tomar 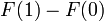 , donde
, donde  y
y  son las fronteras del intervalo [0,1]. (Éste es un ejemplo de una regla general, que dice que para f(x) = xq, con q ≠ −1, la función relacionada, la llamada primitiva es F(x) = (xq+1)/(q+1).) De modo que el valor exacto del área bajo la curva se calcula formalmente como
son las fronteras del intervalo [0,1]. (Éste es un ejemplo de una regla general, que dice que para f(x) = xq, con q ≠ −1, la función relacionada, la llamada primitiva es F(x) = (xq+1)/(q+1).) De modo que el valor exacto del área bajo la curva se calcula formalmente comoHistóricamente, después de que los primeros esfuerzos de definir rigurosamente los infinitesimales no fructificasen, Riemann definió formalmente las integrales como el límite de sumas ponderadas, de forma que el dx sugiere el límite de una diferencia (la anchura del intervalo). La dependencia de la definición de Riemann de los intervalos y la continuidad motivó la aparición de nuevas definiciones, especialmente la integral de Lebesgue, que se basa en la habilidad de extender la idea de "medida" de maneras mucho más flexibles. Así, la notación
Recientemente, los infinitesimales han reaparecido con rigor, a través de innovaciones modernas como el análisis no estándar. Estos métodos no solo reivindican la intuición de los pioneros, también llevan hacia las nuevas matemáticas, y hacen más intuitivo y comprensible el trabajo con cálculo infinitesimal.
A pesar de que hay diferencias entre todas estas concepciones de la integral, hay un solapamiento considerable. Así, el área de la piscina oval se puede hallar como una elipse geométrica, como una suma de infinitesimales, como una integral de Riemann, como una integral de Lebesgue, o como una variedad con una forma diferencial. El resultado obtenido con el cálculo será el mismo en todos los casos.
Definiciones formales
Hay muchas maneras de definir formalmente una integral, no todas equivalentes. Se establecen diferencias para poder abordar casos especiales que no pueden ser integrables con otras definiciones, pero también en ocasiones por razones pedagógicas. Las definiciones más utilizadas de la integral son las integrales de Riemann y las integrales de Lebesgue.Integral de Riemann
Integral con el planteamiento de Riemann hace una suma basada en una partición etiquetada,
con posiciones de muestreo y anchuras irregulares (el máximo en rojo).
El verdadero valor es 3,76; la estimación obtenida es 3,648.
 y denotamos la partición como
y denotamos la partición como 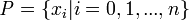
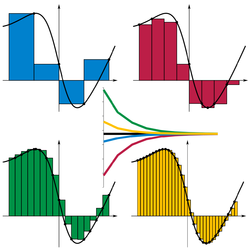
Convergencia de sumatorios de Riemann a medida en que se parten los intervalos, cuando se muestrea a ■ la derecha, ■ el mínimo, ■ el máximo, o ■ la izquierda.
- Para todo ε > 0 existex δ > 0 tal que, para cualquier partición etiquetada [a,b] con paso más pequeño que δ, se tiene
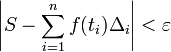 , donde
, donde 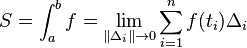
Integral de Darboux
La Integral de Darboux se define en términos de sumas de los siguientes tipos:Llamadas suma inferior y superior respectivamente, donde:
son las alturas de los rectángulos, y xi-xi-1 la longitud de la base de los rectángulos. La integral de Darboux está definida como el único número acotado entre las sumas inferior y superior, es decir,
La interpretación geométrica de la integral de Darboux sería el cálculo del área de la región en [a,b] por el Método exhaustivo. La integral de Darboux de una función f en [a,b] existe si y solo si
Del Teorema de Caracterización que dice que si f es integrable en [a,b] entonces ∀ε>0 ∃ P partición de [a,b] : 0≤U(f,P)-L(f,P)≤ε, evidencia la equivalencia entre las definiciones de Integral de Riemman e Integral de Darboux pues se sigue que7
.
| ARYA, J. C. (2009). Matemáticas aplicadas a la administración. México: Pearson Educacíon. |
| (2015). Integral de una suma (diferencia) de funciones.En: wikiped… Consultado elSábado, 14 de noviembre de 2015 Se encuentra en: https://es.wikipedia.org/wiki/Integraci%C3%B3n |
.png)
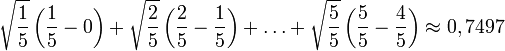
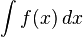
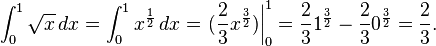



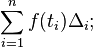

![M_i=\sup\{f(x)|x\in[x_{i-1},x_i]\}, \qquad
m_i=\inf\{f(x)|x\in[x_{i-1},x_i]\}](https://upload.wikimedia.org/math/e/7/6/e76398749ba69dfb83242393b78a082e.png)
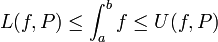
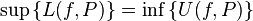



0 comentarios: